Dprime and signal detection theory to locate “weird” participants

In this session we will look at some data that Xin is using in her thesis. Right now she is trying to locate participants who did not take her task seriously. One method for doing so comes from signal detection theory - used to differentiate between random patterns and meaningful patterns. Xin’s task is a lexical decision task, where participants saw either a word or a non-word. They answered whether the word was real by responding YES or NO to each word on the screen.

Xin wants to make sure some participants did not just hit “YES” or “NO” all the way through the experiment.

This week we will continue cleaning and analysing data. Before we start analyzing our data, we want to be make sure that we have valid data. One important step in data cleaning is to remove inattentive participants. How can we tell whether a participant did the task properly or not? Dprime could be a useful tool.

About dprime

Dprime is a measure of sensitivity of responses to a given stimulus. In a study such as Xin’s, there are four possible meanings behind any valid response. We can adapt the Dprime sensitivity index from here to match with Xin’s design:

Dprime(sensitivity index)

              ANSWERED YES    |  ANSWERED NO
 WORD    |     HIT            |  MISS
 NONWORD |     FALSE ALARM    |  CORRECT REJECTION

For Dprime, we care about two of these measures:

Hit Rate (H): proportion of WORD trials to which subject responded YES = P("yes" | word) (the number of times someone answered yes to a word trial / all word trials)

False Alarm rate (FA): proportion of NONWORD trials to which subject responded YES = P("yes" | nonword) (the number of times someone answered yes to a non-word trial / all non-word trials)

Dprime (d’): Z(H)-Z(FA))

Dprime (d’) is caluclated using z-scores and uses the same logic as a z-score, in that a z-score of 1 = one standard deviation from the mean.

Typical d’ values are up to 2.0.

If a participant had 69% accuracy for both words and nonwords, their d’ would be 1.0.

A value of d′ = 0 is chance (“guessing”) performance. interpreting dprime

Main tasks

  1. Calculate the counts for each item type
  2. Pivot wider
  3. Get rid of missing trials
  4. Calculate totals of word trials and non word trials
  5. Calculate the hit rate and false alarm rate
  6. Make the z scores using qnorm()
  7. Calculate dprime
  8. Plot dprime
library(tidyverse)
## ── Attaching core tidyverse packages ────────────────────────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2     
## ── Conflicts ──────────────────────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(ggthemes)

Loading the dataset

You can download the dateset from here or use read_csv() to import the data. The raw dataset can be saved as ‘df’.

df <- read_csv('https://stephenskalicky.com/r_data/dprime_data_raw.csv')
## Rows: 19711 Columns: 38
## ── Column specification ──────────────────────────────────────────────────────────────────────────
## Delimiter: ","
## chr (10): block, word, type, resp, vuw, condition, gender, test, otherL1, deci
## dbl (28): order, rt, list, cycle, sequence, age, score, year, LexTale, cscor...
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

There are loads of variables in the dataset but We will only need three variables today: participant Id (vuw), wordtype (type) and response (resp). Trim down the original dataset to only these variables and save it as ‘df2’.

# tidyverse version
df2 <- df %>%
  dplyr::select(vuw, type, resp)

# base R version
df2 <- subset(df, select=c("vuw", "type", "resp"))

Inspect the “type” and “response” variables by converting them to a factor (use levels(as.factor(x))). How does this data map on to the sensitivity chart above?

levels(as.factor(df2$type))
## [1] "nonword" "word"
levels(as.factor(df2$resp))
## [1] "correct"   "incorrect" "missing"

1. Calculate the counts for each item type

So we need a count of how many times each type of response was given to both words and non-words.
Create a new df named scores from df2. Calculate the raw counts of each type X response combination for each participant.
You’ll need to use group_by(), summarise(), and n().

# tidyverse version
scores.tv <- df2 %>%
  dplyr::group_by(vuw, type, resp) %>%
  dplyr::summarise(n = n())
## `summarise()` has grouped output by 'vuw', 'type'. You can override using the
## `.groups` argument.
# base R
scores.b <- as.data.frame(table(df2))

Your scores df should be like this:

glimpse(scores.tv)
## Rows: 302
## Columns: 4
## Groups: vuw, type [124]
## $ vuw  <chr> "009d3700", "009d3700", "009d3700", "009d3700", "009d3700", "009d…
## $ type <chr> "nonword", "nonword", "nonword", "word", "word", "word", "nonword…
## $ resp <chr> "correct", "incorrect", "missing", "correct", "incorrect", "missi…
## $ n    <int> 92, 65, 1, 151, 12, 1, 111, 47, 133, 29, 1, 103, 55, 152, 12, 83,…

2. Pivot the data wider

To better calculate the proportion of correct and incorrect answers in word and nonword trials, let’s pivot the data into wide format and save it as scores2. The key arguments are names_from and values_from.

# tidyverse
scores2.tv <- scores.tv %>%
  pivot_wider(names_from = c(type, resp), values_from = n)


# base R (probably more efficient)
library(reshape2)
## 
## Attaching package: 'reshape2'
## The following object is masked from 'package:tidyr':
## 
##     smiths
scores2.b <- dcast(df2, vuw ~ type + resp)
## Using resp as value column: use value.var to override.
## Aggregation function missing: defaulting to length

3. Get rid of missing trials & 4. Calculate totals of word trials and non word trials

Remember our formula for hit rate and false alarm rate?

HIT RATE = number of word-correct trials / total number of word trials
FALSE ALARM = number of nonword-incorrect trials / total number of non-word trials

So we don’t need the missing trials. We also need to know the total number of word trials and non-word trials, per participant.

Create a new df named scores3 from scores2.

In a single pipe:
- remove the two columns associated with missing data - create a new column named word_trials which is the sum of all real word trials - create a ner column named nw_trials which is the sum of all non-word trials

# tidyverse version
scores3.tv <- scores2.tv %>%
  dplyr::select(-word_missing, -nonword_missing) %>%
  dplyr::mutate(word_trials = word_correct + word_incorrect, nw_trials = nonword_correct + nonword_incorrect)

# base R version
scores3.b <- subset(scores2.b, select = c(-word_missing, -nonword_missing))

# add total trials
scores3.b$word_trials <- scores3.b$word_correct + scores3.b$word_incorrect
scores3.b$nw_trials <- scores3.b$nonword_correct + scores3.b$nonword_incorrect

5. Calculate the hit rate and false alarm rate

Now we can calculate the hit rate and false alarm rate. Create a new df scores4 from scores3.

Create a new column hit_rate which is the proportion of word-correct / all word trials.

Create a new column named false_alarm which is the proportion of nonword-incorrect / all non-word trials.

# tidyverse version
scores4.tv <- scores3.tv %>%
  #dplyr::mutate(hit_rate = round(word_correct / word_trials*100, 2), false_alarm = nonword_incorrect / nw_trials*100)
  dplyr::mutate(hit_rate = word_correct / word_trials, false_alarm = nonword_incorrect / nw_trials)

# base R
scores4.b <- scores3.b

# guess base R is better
# a shortcut to not have to type x$ is to use with, then it makes it available. 
scores4.b$hit_rate <- with(scores4.b, word_correct / word_trials)
scores4.b$false_alarm <- with(scores4.b, nonword_incorrect / nw_trials)

6. Make the z scores using qnorm() & 7. Calculate dprime

Now we should be able to caclulate our own d prime (d’).

We can use qnorm() to get z scores for our values (because the z-scores actually come from the subtracted product and not the values themselves - don’t worry about this too much - just use qnorm() in your pipe to make the new values.).

Let’s create a df scores5 by adding another three columns to scores4:

  • HRz for the qnorm() of hit rate
  • FAz for qnorm of false alarm rate  
  • dprime for dprime (d' = Z(Hit rate)-Z(False alarm))

8. Plot dprime

Now we can plot the data! Before that, let’s create a df named plot.data as we need hit rate, false alarm rate and dprime only - so select only those columns (this isn’t necessary at all).

# tidyverse
plot.data.tv <- scores5.tv %>%
  ungroup() %>%
  dplyr::select(hit_rate, false_alarm, dprime)

# base R
plot.data.b <- subset(scores5.b, select = c(hit_rate, false_alarm, dprime))

Your ‘plot.data’ should look like this.

head(plot.data.tv)
## # A tibble: 6 × 3
##   hit_rate false_alarm dprime
##      <dbl>       <dbl>  <dbl>
## 1    0.926      0.414    1.67
## 2    0.821      0.297    1.45
## 3    0.927      0.348    1.84
## 4    0.877      0.471    1.23
## 5    0.758      0.149    1.74
## 6    0.938      0.0321   3.39

Time to visualize the data! Create a ggplot with hit rate on the y axis and false alarm rate on the x axis.

Add a geom_text which takes dprime as the label within the aes call. Also add color = dprime outside the aes but within the geom_text call.  

Add theme_gdocs() to the end of your plot.

library(ggthemes)
ggplot(plot.data.b, aes(x = false_alarm, y = hit_rate, label = round(dprime, 2), color = dprime)) +
  geom_text() +
 # xlim(0,1) + 
  #ylim(0,1) +
  coord_cartesian(xlim = c(0,1), ylim = c(0,1)) +
  geom_abline(slope = 1, alpha = .5, color = 'red', linetype = 2) +
  theme_gdocs()

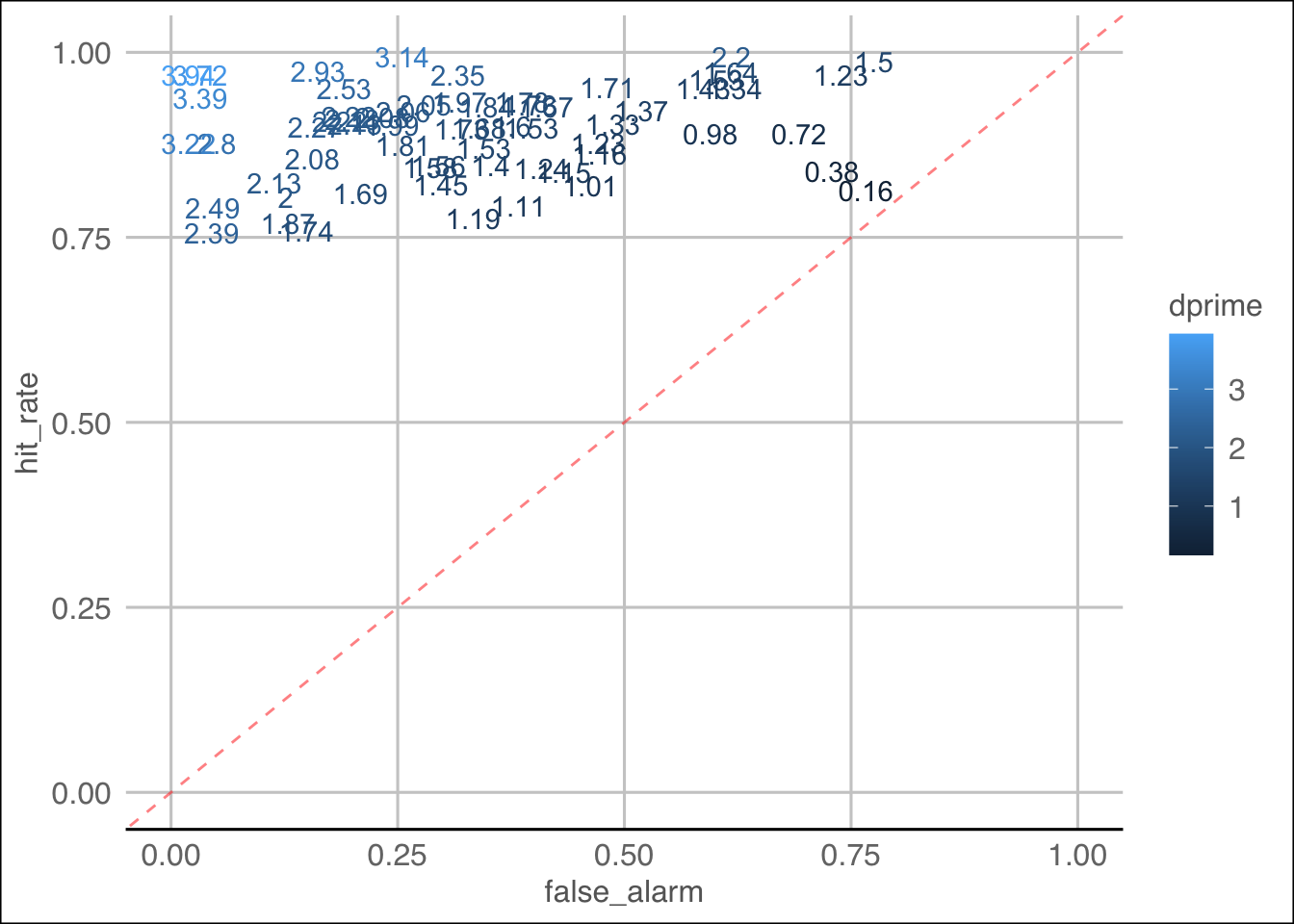
Key observations:

  1. Nature of data shows participants are, in general, pretty good at the real word trials - hit rate is overall quite high
  2. Lots of participants grouped in top right corner which shows that for the most part they are doing ok
  3. Four participants with a dprime < 1, one with near 0 (0.16). However, can we truly know if this is a result of malicious behaviour?
  4. Maybe cluster analysis could help? (shrug)

Conclusion - need to cross reference this to other data, such as RT, longstring, and more.