Ch6.1-6.2

Multiple Regression

We will cover these topics

1. what is multiple regression?

2. how to build a multiple regression model in R

3. how to plot a multiple regression

6.1 Regression with More Than One Predictor

Why do we need multiple regression?

• In multiple regression, we attempt to predict a dependent or response variable \(y\) on the basis of an assumed linear relationship with two or more independent variables \(x_1\), \(x_2\), …, \(x_k\).

A multiple linear regression model can be expressed as

\[ y=β_0 +β_1x_1 +β_2x_2 + ... +β_kx_k + e \]

\(y\) is the dependent variable, \(x_1\), \(x_2\), …, \(x_k\) are independent variables, \(k\) is the number of independent variables, \(\beta_0\), \(\beta_1\) …, \(\beta_k\) are regression coefficients

Example with data

We will use the data from the paper “Which words are most iconic? Iconicity in English sensory words” (Winter et al., 2017).

• Whether word forms resemble their meaning??

  This paper investigated iconicity of English words through the relationship between systematicity and the sensory properties of words. 3001 English words were rated by English native speakers.

• Iconicity as a function of sensory experience

Load the data

• SER - sensory experience, Syst - systematicity, Freq - word frequency, CoreseImag - imageability, Conc - concreteness
• Sensory experiences were rated from 1 to 7. Five common senses were considered (taste, touch, sound, sight and smell)
• Iconicity was rated from -5 to 5

library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

library(broom)

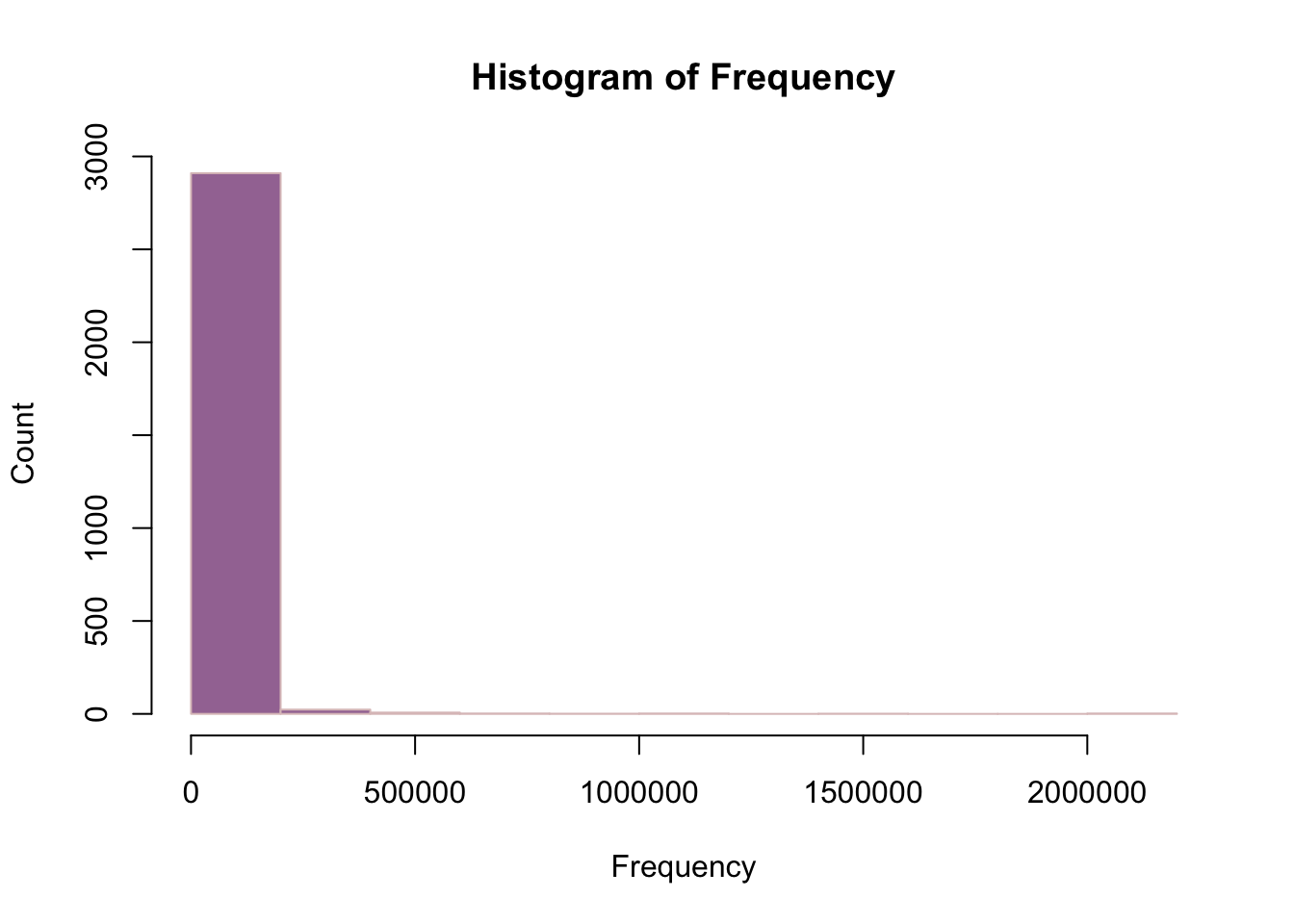
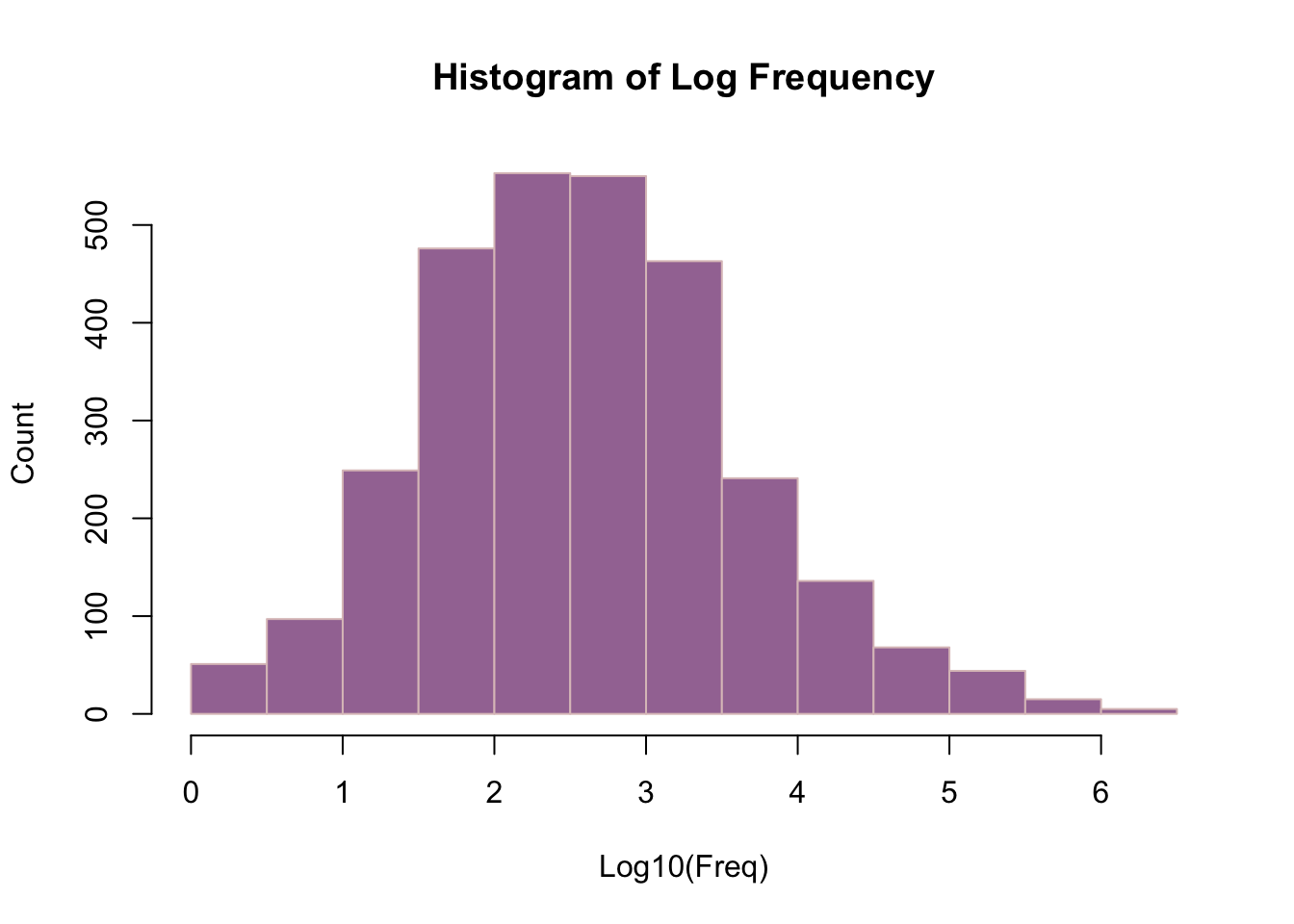
rawdata<- read_csv("winter_2017_iconicity.csv")

Rows: 3001 Columns: 8
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): Word, POS
dbl (6): SER, CorteseImag, Conc, Syst, Freq, Iconicity

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

rawdata %>% print(n=10, width=Inf) # width = Inf is to see all the columns of the tibble

# A tibble: 3,001 × 8
   Word      POS           SER CorteseImag  Conc  Syst    Freq Iconicity
   <chr>     <chr>       <dbl>       <dbl> <dbl> <dbl>   <dbl>     <dbl>
 1 a         Grammatical NA             NA  1.46    NA 1041179     0.462
 2 abide     Verb        NA             NA  1.68    NA     138     0.25 
 3 able      Adjective    1.73          NA  2.38    NA    8155     0.467
 4 about     Grammatical  1.2           NA  1.77    NA  185206    -0.1  
 5 above     Grammatical  2.91          NA  3.33    NA    2493     1.06 
 6 abrasive  Adjective   NA             NA  3.03    NA      23     1.31 
 7 absorbent Adjective   NA             NA  3.1     NA       8     0.923
 8 academy   Noun        NA             NA  4.29    NA     633     0.692
 9 accident  Noun        NA             NA  3.26    NA    4146     1.36 
10 accordion Noun        NA             NA  4.86    NA      67    -0.455
# ℹ 2,991 more rows

range(rawdata$Iconicity, na.rm=TRUE)

[1] -2.800000  4.466667

# counting missing data in each dependent variable 
not_missing_imag<- sum(is.na(rawdata$CorteseImag))
not_missing_SER <- sum(is.na(rawdata$SER))
not_missing_Conc <- sum(is.na(rawdata$Conc))
not_missing_syst <- sum(is.na(rawdata$Syst))
not_missing_freq <- sum(is.na(rawdata$Freq))
not_missing_iconicity <- sum(is.na(rawdata$Iconicity))

not_missing_imag

[1] 1828

not_missing_SER

[1] 1222

not_missing_Conc

[1] 181

not_missing_syst

[1] 1898

not_missing_freq

[1] 53

not_missing_iconicity

[1] 0

most_iconic<- rawdata %>% mutate(Iconicity = round(Iconicity,3)) %>% 
  filter(Iconicity==max(Iconicity))
least_iconic <-rawdata %>% mutate(Iconicity = round(Iconicity,3)) %>% 
  filter(Iconicity==min(Iconicity))
most_iconic

# A tibble: 1 × 8
  Word    POS     SER CorteseImag  Conc  Syst  Freq Iconicity
  <chr>   <chr> <dbl>       <dbl> <dbl> <dbl> <dbl>     <dbl>
1 humming Verb     NA          NA  4.17    NA   251      4.47

least_iconic

# A tibble: 1 × 8
  Word      POS     SER CorteseImag  Conc  Syst  Freq Iconicity
  <chr>     <chr> <dbl>       <dbl> <dbl> <dbl> <dbl>     <dbl>
1 dandelion Noun     NA          NA     5    NA    15      -2.8

Pre-processing the Data

• Log transform the word frequencies

# Log transform the frequency

p1_freq= hist(rawdata$Freq,
              main = "Histogram of Frequency",
              xlab= "Frequency",
              ylab= "Count",
              col="#A376A2",
              border="#DDC3C3")

• The raw frequency data is extremely skewed, therefore, we need to log transform the frequency data

rawdata <- mutate(rawdata, logfreq=log10(Freq))
p2_logfreq= hist(rawdata$logfreq,
                 main = "Histogram of Log Frequency",
                 xlab= "Log10(Freq)",
                 ylab= "Count",
                 col="#A376A2",
                 border="#DDC3C3")

Magically, the log transformed frequency data are normally distributed!

Build the Model

Now let’s build the multiple regression model.

model1 <- lm (Iconicity~ SER + CorteseImag + Syst + logfreq, data= rawdata)
glance(model1)

# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.212         0.209  1.00      66.4 9.79e-50     4 -1403. 2817. 2846.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

summary(model1)

Call:
lm(formula = Iconicity ~ SER + CorteseImag + Syst + logfreq, 
    data = rawdata)

Residuals:
     Min       1Q   Median       3Q      Max 
-3.07601 -0.71411 -0.03824  0.67337  2.76066 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   1.54476    0.18795   8.219 6.43e-16 ***
SER           0.49713    0.04012  12.391  < 2e-16 ***
CorteseImag  -0.26328    0.02500 -10.531  < 2e-16 ***
Syst        401.52431  262.90268   1.527    0.127    
logfreq      -0.25163    0.03741  -6.725 2.97e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.002 on 984 degrees of freedom
  (2012 observations deleted due to missingness)
Multiple R-squared:  0.2125,    Adjusted R-squared:  0.2093 
F-statistic: 66.36 on 4 and 984 DF,  p-value: < 2.2e-16

Check R squared

The model explained about 21% of the variation in iconicity ratings.

glance(model1)$r.squared

[1] 0.2124559

Check coefficients

We can use round() to round the coefficients to make them easier for explanation.

• round() takes two arguments, 1) a vector of numbers, 2) a number indicating to how many decimals the vector should be rounded to.

tidy (model1) %>% select(term, estimate) %>% mutate (estimate= round(estimate, 2))

# A tibble: 5 × 2
  term        estimate
  <chr>          <dbl>
1 (Intercept)     1.54
2 SER             0.5 
3 CorteseImag    -0.26
4 Syst          402.  
5 logfreq        -0.25

Based on the estimates, a predictive equation can be as

\[ \text{iconicity} = 1.54 + 0.50 * \text{SER} + (-0.26) * \text{CorteseImag} + 401.52 * \text{Syst} + (-0.25) * \text{logfreq} \]

• What is the the strongest predictor from this result?

• One-unit change of systematicity leads to 401.5 change on the iconicity rating.

Caution

• What does a one-unit change mean for systematicity?
• What does a one-unit change mean for frequency?

range(rawdata$Syst, na.rm=TRUE)

[1] -0.000481  0.000641

Standardization !!

To make the independent variables more comparable!

st_data<- mutate(rawdata,
                 SER_st=scale(SER),
                 CorteseImag_st= scale(CorteseImag),
                 Syst_st=scale(Syst),
                 Freq_st=scale(logfreq))

Re-build the model

model2<- lm(Iconicity~SER_st+CorteseImag_st+Syst_st+Freq_st, data=st_data)
summary(model2)

Call:
lm(formula = Iconicity ~ SER_st + CorteseImag_st + Syst_st + 
    Freq_st, data = st_data)

Residuals:
     Min       1Q   Median       3Q      Max 
-3.07601 -0.71411 -0.03824  0.67337  2.76066 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)     1.25694    0.03612  34.801  < 2e-16 ***
SER_st          0.51550    0.04160  12.391  < 2e-16 ***
CorteseImag_st -0.39364    0.03738 -10.531  < 2e-16 ***
Syst_st         0.04931    0.03229   1.527    0.127    
Freq_st        -0.26004    0.03867  -6.725 2.97e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.002 on 984 degrees of freedom
  (2012 observations deleted due to missingness)
Multiple R-squared:  0.2125,    Adjusted R-squared:  0.2093 
F-statistic: 66.36 on 4 and 984 DF,  p-value: < 2.2e-16

Important

R-square value DID NOT change!

Standardization DID NOT change the underlying model!

• What does one-unit change of sensory experience mean?

• It means “For each increase in sensory experience by 1 STD, iconicity rating increases by 0.5”.

Plots

plot(model2)

• In the first plot, we want to see the red line be as horizontal as possible, to indicate that the only variation left in the data is due to the unexplained errors.

• The second plot is to check if the residuals are normally distributed.

• The third plot is to see how far individual values are from the regression line. Again we want to see a horizontal red line with no particular patterns.

• The fourth plot is to check outliers.

Plot one variable

library (car)

Loading required package: carData

Attaching package: 'car'

The following object is masked from 'package:dplyr':

    recode

The following object is masked from 'package:purrr':

    some

avPlots(model2)

Reference

Note

Data for Statistics For Linguistics: An Introduction Using R, can be downloaded here.

https://osf.io/34mq9/files/osfstorage

Downloads

Download notebook and data 

Download a reveal.js slide deck